Understanding Directed Graphs in Python

In this blog post, we’ll dive into implementing and working with a Directed Graph using Python. We'll also walk through basic components such as edges, adjacency lists, and traversal.

A Directed Graph (or Digraph) is a set of nodes connected by edges, where the edges have a direction - meaning they go from one node to another.

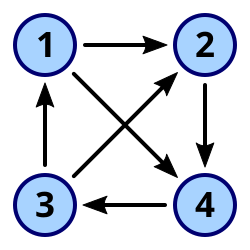
Source: Wikipedia – Directed Graph

🛠️ Here's how you can build a simple directed graph class in Python using an adjacency list:

class Graph:
    def __init__(self, vno):
        self.vertex_count = vno
        self.adj_list = {v: [] for v in range(vno)}

    def add_edge(self, u, v, weight=1):
        if 0 <= u < self.vertex_count and 0 <= v < self.vertex_count:
            self.adj_list[u].append((v, weight))

    def print_graph(self):
        for vertex, neighbor in self.adj_list.items():
            print(f'Vertex {vertex} : {neighbor}')

🔍 In the above code:

• add_edge(u, v) adds a directed edge from node u to node v.
• The adjacency list stores a list of tuples representing neighbors and weights for each vertex.

🧪 Let's test it with a few nodes and connections:

if __name__ == "__main__":
    graph = Graph(4)
    graph.add_edge(0, 1)
    graph.add_edge(0, 2)
    graph.add_edge(2, 3)
    graph.print_graph()

✅ Expected Output:

Vertex 0 : [(1, 1), (2, 1)]
Vertex 1 : []
Vertex 2 : [(3, 1)]
Vertex 3 : []

🎯 Key Takeaways:

• Directed graphs only connect one way: (u -> v).
• No edge from v -> u is assumed unless explicitly added.
• Useful in scenarios like Dependency trees, Social Networking Branches (followers), or building routing systems.

🔗 Source Code: GitHub Repository